MICROWAVE WAVEGUIDES
and COAXIAL CABLES
 In general, a waveguide consists of a hollow metallic tube
of arbitrary cross section uniform in extent in the direction of propagation.
Common waveguide shapes are rectangular, circular, and ridged. The rectangular
waveguide has a width "a" and height "b" as shown in figure 1.
In general, a waveguide consists of a hollow metallic tube
of arbitrary cross section uniform in extent in the direction of propagation.
Common waveguide shapes are rectangular, circular, and ridged. The rectangular
waveguide has a width "a" and height "b" as shown in figure 1.
Commonly used rectangular waveguides have an aspect ratio b/a of
approximately 0.5. Such an aspect ratio is used to preclude generation of field
variations with height and their attendant unwanted modes. Waveguides are used
principally at frequencies in the microwave range; inconveniently large guides
would be required to transmit radio-frequency power at longer wavelengths. In
the X-Band frequency range of 8.2 to 12.4 GHz, for example, the U.S. standard
rectangular waveguide, WR-90, has an inner width of 2.286 cm (0.9 in.) and an
inner height of 1.016 cm (0.4 in.).
In waveguides the electric and magnetic fields are confined to the space
within the guides. Thus no power is lost to radiation. Since the guides are
normally filled with air, dielectric losses are negligible. However, there is
some I2R power lost to heat in the walls of the guides, but this loss
is usually very small.
It is possible to propagate several modes of electromagnetic waves within a
waveguide. The physical dimensions of a waveguide determine the cutoff frequency
for each mode. If the frequency of the impressed signal is above the cutoff
frequency for a given mode, the electromagnetic energy can be transmitted
through the guide for that particular mode with minimal attenuation. Otherwise
the electromagnetic energy with a frequency below cutoff for that particular
mode will be attenuated to a negligible value in a relatively short distance.
This grammatical use of cutoff frequency is opposite that used for coaxial
cable, where cutoff frequency is for the highest useable frequency. The dominant
mode in a particular waveguide is the mode having the lowest cutoff frequency.
For rectangular waveguide this is the TE10 mode. The TE (transverse electric)
signifies that all electric fields are transverse to the direction of
propagation and that no longitudinal electric field is present. There is a
longitudinal component of magnetic field and for this reason the TEmn
waves are also called Hmn waves. The TE designation is usually
preferred. Figure 2 shows a graphical depiction of the E field variation in a
waveguide for the TE10, TE20, and TE30 modes.
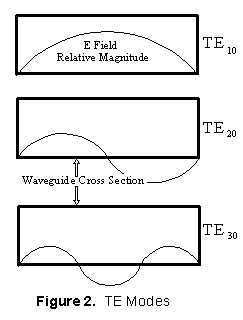 As can be seen, the first index indicates the number of half
wave loops across the width of the guide and the second index, the number of
loops across the height of the guide - which in this case is zero. It is
advisable to choose the dimensions of a guide in such a way that, for a given
input signal, only the energy of the dominant mode can be transmitted through
the guide. For example, if for a particular frequency, the width of a
rectangular guide is too large, then the TE20 mode can propagate causing a
myriad of problems. For rectangular guides of low aspect ratio the TE20 mode is
the next higher order mode and is harmonically related to the cutoff frequency
of the TE10 mode. It is this relationship together with attenuation and
propagation considerations that determine the normal operating range of
rectangular waveguide.
As can be seen, the first index indicates the number of half
wave loops across the width of the guide and the second index, the number of
loops across the height of the guide - which in this case is zero. It is
advisable to choose the dimensions of a guide in such a way that, for a given
input signal, only the energy of the dominant mode can be transmitted through
the guide. For example, if for a particular frequency, the width of a
rectangular guide is too large, then the TE20 mode can propagate causing a
myriad of problems. For rectangular guides of low aspect ratio the TE20 mode is
the next higher order mode and is harmonically related to the cutoff frequency
of the TE10 mode. It is this relationship together with attenuation and
propagation considerations that determine the normal operating range of
rectangular waveguide.
The discussion on circular waveguides will not be included because they are
rarely used in the EW area. Information regarding circular waveguides can be
found in numerous textbooks on microwaves.
CHARACTERISTICS OF STANDARD RECTANGULAR WAVEGUIDES
Rectangular waveguides are commonly used for power transmission at microwave
frequencies. Their physical dimensions are regulated by the frequency of the
signal being transmitted. Table 1 tabulates the characteristics of the standard
rectangular waveguides. It may be noted that the number following the EIA prefix
"WR" is in inside dimension of the widest part of the waveguide, i.e. WR90 has
an inner dimension of 0.90".
Table 1. Rectangular Waveguide Specifications
| Waveguide Size |
JAN WG
Desig |
MIL-W-85 Dash # |
Material |
Freq Range (GHz) |
Freq Cutoff (GHz) |
Power
(at 1 Atm) |
Insertion Loss
(dB/100ft) |
Dimensions (Inches) |
| Outside |
Wall Thickness |
| CW |
Peak |
| WR284 |
RG48/U
RG75/U |
1-039
1-042 |
Copper
Aluminum |
2.60 - 3.95 |
2.08 |
45
36 |
7650 |
.742-.508
1.116-.764 |
3.000x1.500 |
0.08 |
| WR229 |
RG340/U
RG341/U |
1-045
1-048 |
Copper
Aluminum |
3.30 - 4.90 |
2.577 |
30
24 |
5480 |
.946-.671
1.422-1.009 |
2.418x1.273 |
0.064 |
| WR187 |
RG49/U
RG95/U |
1-051
1-054 |
Copper
Aluminum |
3.95 - 5.85 |
3.156 |
18
14.5 |
3300 |
1.395-.967
2.097-1.454 |
1.000x1.000 |
0.064 |
| WR159 |
RG343/U
RG344/U |
1-057
1-060 |
Copper
Aluminum |
4.90 - 7.05 |
3.705 |
15
12 |
2790 |
1.533-1.160
2.334-1.744 |
1.718x0.923 |
0.064 |
| WR137 |
RG50/U
RG106/U |
1-063
1-066 |
Copper
Aluminum |
5.85 - 8.20 |
4.285 |
10
8 |
1980 |
1.987-1.562
2.955-2.348 |
1.500x0.750 |
0.064 |
| WR112 |
RG51/U
RG68/U |
1-069
1-072 |
Copper
Aluminum |
7.05 - 10.0 |
5.26 |
6
4.8 |
1280 |
2.776-2.154
4.173-3.238 |
1.250x0.625 |
0.064 |
| WR90 |
RG52/U
RG67/U |
1-075
1-078 |
Copper
Aluminum |
8.2 - 12.4 |
6.56 |
3
2.4 |
760 |
4.238-2.995
6.506-4.502 |
1.000x0.500 |
0.05 |
| WR75 |
RG346/U
RG347/U |
1-081
1-084 |
Copper
Aluminum |
10.0 - 15.0 |
7.847 |
2.8
2.2 |
620 |
5.121-3.577
7.698-5.377 |
0.850x0.475 |
0.05 |
| WR62 |
RG91/U
RG349/U |
1-087
1-091 |
Copper
Aluminum |
12.4 - 18.0 |
9.49 |
1.8
1.4 |
460 |
6.451-4.743
9.700-7.131 |
0.702x0.391 |
0.04 |
| WR51 |
RG352/U
RG351/U |
1-094
1-098 |
Copper
Aluminum |
15.0 - 22.0 |
11.54 |
1.2
1 |
310 |
8.812-6.384
13.250-9.598 |
0.590x0.335 |
0.04 |
| WR42 |
RG53/U |
1-100 |
Copper |
18.0 - 26.5 |
14.08 |
0.8 |
170 |
13.80-10.13 |
0.500x0.250 |
0.04 |
| WR34 |
RG354/U |
1-107 |
Copper |
2.0 - 33.0 |
17.28 |
0.6 |
140 |
16.86-11.73 |
0.420x0.250 |
0.04 |
| WR28 |
RG271/U |
3-007 |
Copper |
26.5 - 40.0 |
21.1 |
0.5 |
100 |
23.02-15.77 |
0.360x0.220 |
0.04 |
DOUBLE RIDGE RECTANGULAR WAVEGUIDE
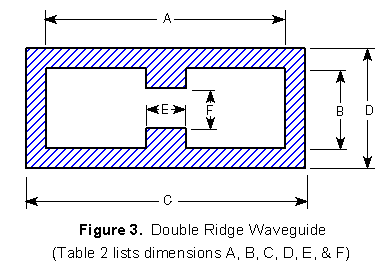 Another type of waveguide commonly used in EW systems is the
double ridge rectangular waveguide shown in figure3. The ridges in this
waveguide increase the bandwidth of the guide at the expense of higher
attenuation and lower power-handling capability. The bandwidth can easily exceed
that of two contiguous standard waveguides. Introduction of the ridges mainly
lowers the cutoff frequency of the TE10 mode from that of the unloaded guide,
which is predicated on width alone. The reason for this can easily be explained
when the field configuration in the guide at cutoff is investigated. At cutoff
there is no longitudinal propagation down the guide. The waves simply travel
back and forth between the side walls of the guide. In fact the guide can be
viewed as a composite parallel plate waveguide of infinite width where the width
corresponds to the direction of propagation of the normal guide.
Another type of waveguide commonly used in EW systems is the
double ridge rectangular waveguide shown in figure3. The ridges in this
waveguide increase the bandwidth of the guide at the expense of higher
attenuation and lower power-handling capability. The bandwidth can easily exceed
that of two contiguous standard waveguides. Introduction of the ridges mainly
lowers the cutoff frequency of the TE10 mode from that of the unloaded guide,
which is predicated on width alone. The reason for this can easily be explained
when the field configuration in the guide at cutoff is investigated. At cutoff
there is no longitudinal propagation down the guide. The waves simply travel
back and forth between the side walls of the guide. In fact the guide can be
viewed as a composite parallel plate waveguide of infinite width where the width
corresponds to the direction of propagation of the normal guide.
The TE10 mode cutoff occurs where this composite guide has its lowest-order
resonant frequency. This occurs when there is only one E field maximum across
the guide which occurs at the center for a symmetrical ridge. Because of the
reduced height of the guide under the ridge, the effective TE10 mode resonator
is heavily loaded as though a shunt capacitor were placed across it. The cutoff
frequency is thus lowered considerably. For the TE20 mode the fields in the
center of the guide will be at a minimum. Therefore the loading will have a
negligible effect. For guides of proper aspect ratio, ridge height, and ridge
width, an exact analysis shows that the TE10 mode cutoff can be lowered
substantially at the same time the TE20 and TE30 mode cutoffs are raised
slightly.
In the case of ridged waveguides, in the EIA designation, (WRD350 D36) the
first "D" stands for double ridged ("S" for single ridged), the 350 is the
starting frequency (3.5 GHz), and the "D36" indicates a bandwidth of 3.6:1. The
physical dimensions and characteristics of a WRD350 D24 and WRD350 D36 are
radically different. A waveguide with a MIL-W-23351 dash number beginning in 2
(i.e. 2-025) is a double ridge 3.6:1 bandwidth waveguide. Likewise a 1- is a
single ridge 3.6:1, a 3- is a single ridge 2.4:1, and a 4- is a double ridge
2.4:1 waveguide.
Table 2 shows double ridged waveguide specifications.
Table 2. Double Ridge Rectangular Waveguide Specifications
| Waveguide Size |
MIL-W- 23351 Dash # |
Material |
Freq Range (GHz) |
Freq Cutoff (GHz) |
Power
(at 1 Atm) |
Insertion Loss (dB/ft) |
Dimensions (Inches) |
| CW |
Peak |
A |
B |
C |
D |
E |
F |
| WRD250 |
- |
Alum
Brass
Copper
Silver Al |
2.60 -
7.80 |
2.093 |
24 |
120 |
0.025
0.025
0.018
0.019 |
1.655 |
0.715 |
2 |
1 |
0.44 |
0.15 |
WRD350
D24 |
4-029
4-303
4-031 |
Alum
Brass
Copper |
3.50 -
8.20 |
2.915 |
18 |
150 |
0.0307
0.0303
0.0204 |
1.48 |
0.688 |
1.608 |
0.816 |
0.37 |
0.292 |
WRD475
D24 |
4-033
4-034
4-035 |
Alum
Brass
Copper |
4.75 -
11.00 |
3.961 |
8 |
85 |
0.0487
0.0481
0.0324 |
1.09 |
0.506 |
1.19 |
0.606 |
0.272 |
0.215 |
WRD500
D36 |
2-025
2-026
2-027 |
Alum
Brass
Copper |
5.00 -
18.00 |
4.222 |
4 |
15 |
0.146
0.141
0.095 |
0.752 |
0.323 |
0.852 |
0.423 |
0.188 |
0.063 |
| WRD650 |
- |
Alum
Brass
Copper |
6.50 -
18.00 |
5.348 |
4 |
25 |
0.106
0.105
0.07 |
0.721 |
0.321 |
0.821 |
0.421 |
0.173 |
0.136 |
WRD750
D24 |
4-037
4-038
4-039 |
Alum
Brass
Copper |
7.50 -
18.00 |
6.239 |
4.8 |
35 |
0.0964
0.0951
0.0641 |
0.691 |
0.321 |
0.791 |
0.421 |
0.173 |
0.136 |
WRD110
D24 |
4-041
4-042
4-043 |
Alum
Brass
Copper |
11.00 -
26.50 |
9.363 |
1.4 |
15 |
0.171
0.169
0.144 |
0.471 |
0.219 |
0.551 |
0.299 |
0.118 |
0.093 |
WRD180
D24 |
4-045
4-046
4-047 |
Alum
Brass
Copper |
18.00 -
40.00 |
14.995 |
0.8 |
5 |
0.358
0.353
0.238 |
0.288 |
0.134 |
0.368 |
0.214 |
0.072 |
0.057 |
Figure 4 shows a comparison of the frequency /attenuation characteristics of
various waveguides. The attenuation is based on real waveguides which is higher
than the theoretical values listed in Tables 1 and 2.
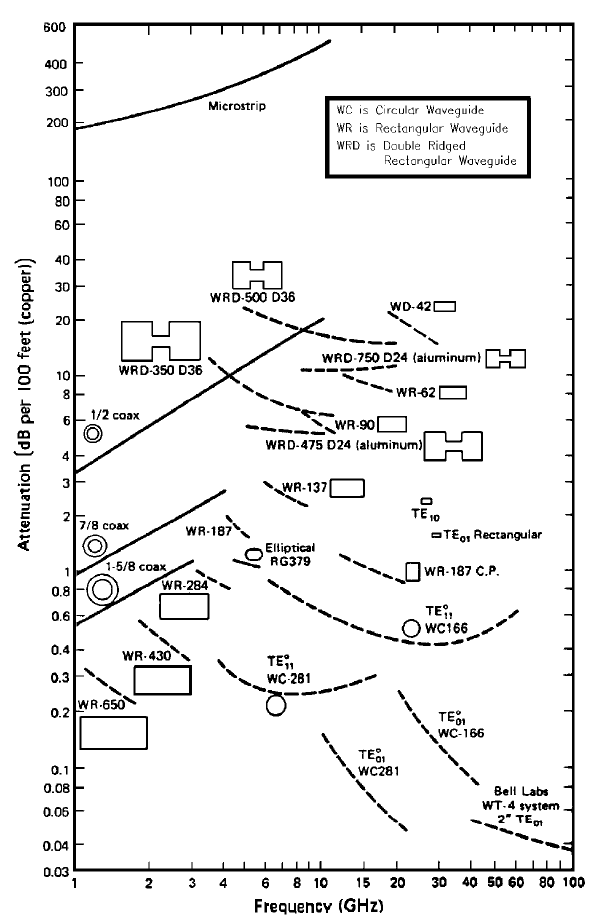
Figure 4. Attenuation vs Frequency for Several Waveguides and
Cables
Figure 5 shows attenuation characteristics of various RF coaxial
cables.
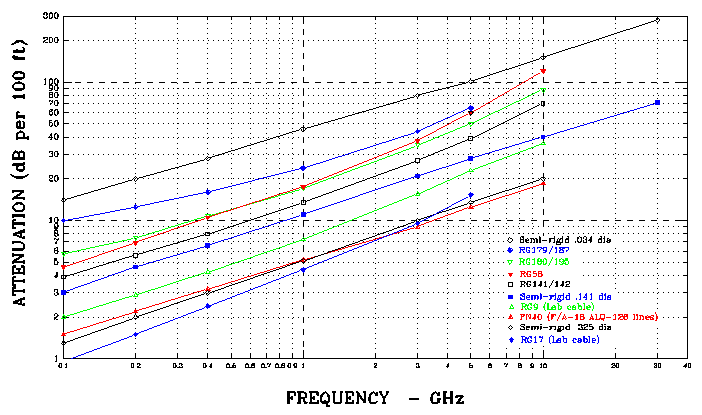
Figure 5. Attenuation vs Frequency for Several Coaxial
Cables
 In general, a waveguide consists of a hollow metallic tube
of arbitrary cross section uniform in extent in the direction of propagation.
Common waveguide shapes are rectangular, circular, and ridged. The rectangular
waveguide has a width "a" and height "b" as shown in figure 1.
In general, a waveguide consists of a hollow metallic tube
of arbitrary cross section uniform in extent in the direction of propagation.
Common waveguide shapes are rectangular, circular, and ridged. The rectangular
waveguide has a width "a" and height "b" as shown in figure 1. As can be seen, the first index indicates the number of half
wave loops across the width of the guide and the second index, the number of
loops across the height of the guide - which in this case is zero. It is
advisable to choose the dimensions of a guide in such a way that, for a given
input signal, only the energy of the dominant mode can be transmitted through
the guide. For example, if for a particular frequency, the width of a
rectangular guide is too large, then the TE20 mode can propagate causing a
myriad of problems. For rectangular guides of low aspect ratio the TE20 mode is
the next higher order mode and is harmonically related to the cutoff frequency
of the TE10 mode. It is this relationship together with attenuation and
propagation considerations that determine the normal operating range of
rectangular waveguide.
As can be seen, the first index indicates the number of half
wave loops across the width of the guide and the second index, the number of
loops across the height of the guide - which in this case is zero. It is
advisable to choose the dimensions of a guide in such a way that, for a given
input signal, only the energy of the dominant mode can be transmitted through
the guide. For example, if for a particular frequency, the width of a
rectangular guide is too large, then the TE20 mode can propagate causing a
myriad of problems. For rectangular guides of low aspect ratio the TE20 mode is
the next higher order mode and is harmonically related to the cutoff frequency
of the TE10 mode. It is this relationship together with attenuation and
propagation considerations that determine the normal operating range of
rectangular waveguide. Another type of waveguide commonly used in EW systems is the
double ridge rectangular waveguide shown in figure3. The ridges in this
waveguide increase the bandwidth of the guide at the expense of higher
attenuation and lower power-handling capability. The bandwidth can easily exceed
that of two contiguous standard waveguides. Introduction of the ridges mainly
lowers the cutoff frequency of the TE10 mode from that of the unloaded guide,
which is predicated on width alone. The reason for this can easily be explained
when the field configuration in the guide at cutoff is investigated. At cutoff
there is no longitudinal propagation down the guide. The waves simply travel
back and forth between the side walls of the guide. In fact the guide can be
viewed as a composite parallel plate waveguide of infinite width where the width
corresponds to the direction of propagation of the normal guide.
Another type of waveguide commonly used in EW systems is the
double ridge rectangular waveguide shown in figure3. The ridges in this
waveguide increase the bandwidth of the guide at the expense of higher
attenuation and lower power-handling capability. The bandwidth can easily exceed
that of two contiguous standard waveguides. Introduction of the ridges mainly
lowers the cutoff frequency of the TE10 mode from that of the unloaded guide,
which is predicated on width alone. The reason for this can easily be explained
when the field configuration in the guide at cutoff is investigated. At cutoff
there is no longitudinal propagation down the guide. The waves simply travel
back and forth between the side walls of the guide. In fact the guide can be
viewed as a composite parallel plate waveguide of infinite width where the width
corresponds to the direction of propagation of the normal guide.
